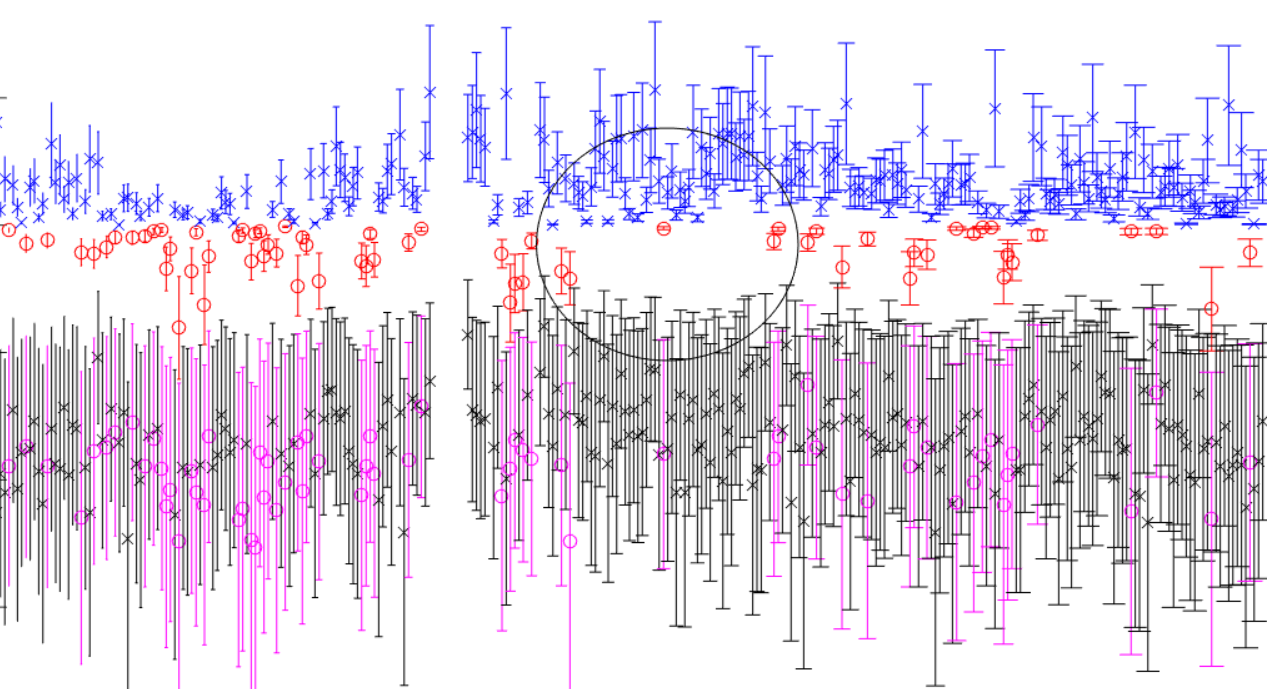
Because nonlinear systems are inherently depending on initial conditions it is tempting to surmise that they might never be able to synchronize. In fact, nonlinear systems do synchronize by assuming trajectories on a common invariant manifold that is a subset of system attractors. The Lyapunov exponent is the gold standard for determination of nonlinear behavior. A positive Lyapunov exponent in a single system suggests that the trajectory of the system is changing and that the system is prone to exhibiting nonlinear dynamics. The conditional Lyapunov exponent is a measure of the tendency of two systems to assume and maintain common behavior. A negative largest conditional Lyapunov exponent means the systems are maintaining trajectory. A positive CLE suggests the systems are divergent and not synchronized.

In the above figure we estimated the Lyapunov spectrum on two time series from a client’s process. Note that there are a lot of red points indicating that the systems are typically synchronized. In the vicinity of the black circle there is a conspicuous absence of red points indicating a period of possible desynchronization. This corresponded temporally with an interruption of process and was ultimately determined to be due to a brief surge in electrical noise that decoupled the systems.